極値統計学の考え方

　大雨、洪水、台風、ハリケーン、干ばつ、熱波、寒波などのめったに起こらないイベント（異常気象・極端気象）を扱う学問は「極値統計学」と呼ばれ、マスコミでもしばしば報道されている。しかし、極値統計学から得られた結果には不確実性があり、異常気象の起こる原因を特定したり、何年に１度起こりうるかを正確に予測することは難しい。

１.「記録的な大雨」をどう解釈するか？

　近年、地球温暖化の進行に伴う極端現象の増加とそれに伴う災害への社会の関心が高まっている。台風災害についていえば、「100年に1度の記録的な大雨」「未曾有の豪雨」、「これまで経験したことのない大雨」、「観測史上最大の雨」などの表現も頻繁に目にする。例えば、2018年に広島県に土石流を引き起こした豪雨は、「未曾有の豪雨」だという。アメダスの観測網が整備されたのは1970年代以降なので、そこから50年間でいえば確かにこの大雨は「観測史上初」であった。しかし、さらに遡って100年の間に起こった大雨の事例を見てみると、実はそこまで珍しくはない。
　例えば、広島測候所が1926年の豪雨による被害を報告しているが、このときの雨量は2018年の豪雨よりも大きく、今でも広島地方気象台の最大記録になっている。さらに、広島県内の水害の石碑によると1907年（明治40年）に起こった大雨により土石流が発生し、多くの犠牲者が出たという^注1）。このように、たとえ観測史上初であろうと歴史に残るような顕著な気象現象かどうか、また地球温暖化が影響しているのかどうかなどを判断する上では注意が必要である^注2）。
　本稿では、関東甲信越から東北地方に大雨をもたらし各地で災害を引き起こした東日本台風を例に極値統計学の考え方を解説する。

２.極値統計学

　極値統計学とは、気象要素などの年最大値データを用いて、これまでに経験した現象やそれらを超える規模の現象がどのくらいの頻度（再現期間）で発生するかを統計的手法により合理的に推定しようとするものである^注3）。再現期間T年の事象が1 年間に起きる確率（超過確率）は、1/Tである。一般に、リスクは異常に大きな（または小さな）値が観測されたときに発生する。そのため、全観測データの平均ではなく非常に大きな（または小さな）値の変動が重要である。数式をあてはめてデータを適切に再現できれば、このような変動を「ある長い期間あるいは広い領域である大きな値が平均1回出現する確率」として予測することができる。古典的な再現期間の導出方法としては、観測データの最大値を取って機械的に大きい順に並べ、順位を再現期間の関数に変換し、それらに適合する関数を見出すというものである（図1）。Gumbel分布（二重指数分布、Hazen plot）の例では、M年間のデータを大きい方からj番目のデータの再現期間 T=M⁄(j-0.5) により計算できる。実験室のような理想的な条件とはほど遠い野外の観測データ（図1a）が、このような単純な変換によりおおむね一直線上に並ぶ（図1c）という事実にはちょっとした驚きもある。
　極値分布の関数形は、理論的にはGumbel分布、Fréchet分布、そしてWeibull分布の3種類のどれかになることがわかっており、これらを統合した関数を一般化極値分布（GEV：Generalized Extreme Value distribution）と呼ぶ。現実のデータは、必ずしもGEVの成立条件を満たさない場合もあるため、様々な分布関数を用意してデータに最も適合するものを選ぶという方法もある。極値統計の理論背景や数学的記述には難しさがあるが、最近はデータと一致するような分布型を見出すプログラムも公開されており、再現期間自体は誰でも推定できるようになっている。ただし、後述するように得られた結果が必ずしも正しく信頼性が高いものであるという保証はない。

図1　Gumbel分布を仮定した場合の彦根地方気象台を例とした年最大日降水量の(a)時系列データを(b)昇順に並べて(c)再現期間（超過確率）を推計する手順。(c)の赤直線は、統計的に導出されたものではなく説明のための目視によるフィッティング。

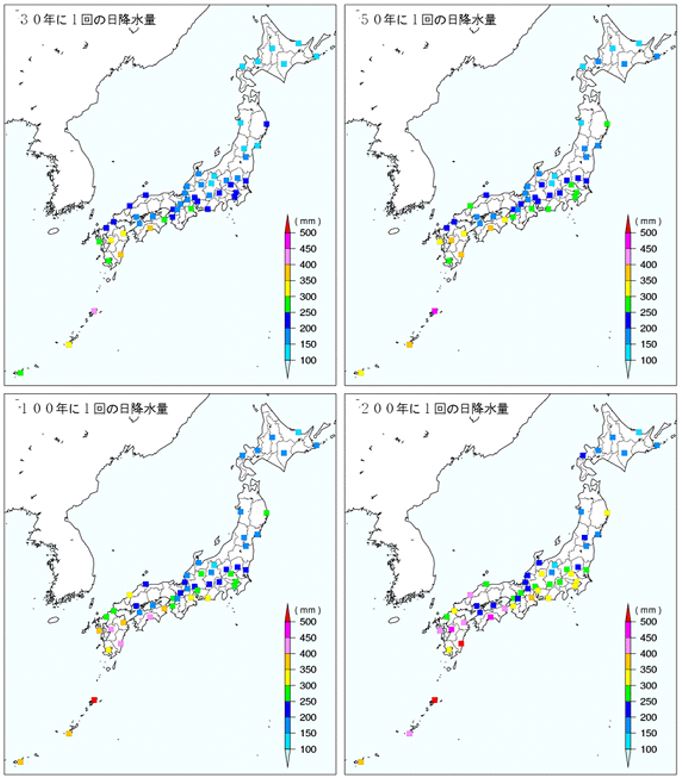
　この理論は20世紀中頃までに基礎が作られ、Gumbel (1958)^注4）の出版後、工学（材料・腐食・土木・建築・信頼性など）の分野では早くから建物や堤防の設計に必要な風速や降水量などの再現期間の推定に利用されてきた（例えば、水谷（2012）^注5））。その後、異常気象への関心が高まり、気象学・水文学・地球科学などの分野でもリスクマップが作成されるようになった。例えば、気象庁は2006年に大規模な災害に備えるための記録的な大雨（確率雨量または確率降水量）のリスクマップを出している（図2）。気象庁では、気温や降水量の異常を判断する再現期間を30年としているが、どの再現期間で比較しても、多雨地域の九州・四国などの方が非多雨地域の東北・北海道よりも確率雨量が大きい傾向が見られる。このように、地域ごとの再現期間に応じて起こりうる大雨の規模を推定できれば、治水や洪水の防御計画を合理的に策定できるというわけだ^注6）。

図2　全国51地点における1901年から2006年の年最大日降水量のデータから推定した確率降水量の分布図^注7）。再現期間：30年・50年・100年・200年。

３.「100年に1度」の不確実性

　さて、図2で示した再現期間のマップは便利そうであるが、どの程度信頼してよいのだろうか？現在の極値統計学の理論には、大きく分けて3つの不確実性がある^注8）：

（１）

データが有限であることによるデータそのものの確率変動。降水量や土砂災害の極値統計解析に使用される過去のデータは数10年程度であることが多く、それを超える期間（例えば、100年）の再現期間に対しては信頼性が低い。

（２）

大雨の例でいえば、「日ごとの降水イベントは独立である」という極値理論の前提は成り立たない場合が多い。

（３）

「気候状態が定常である」という極値理論の前提は成り立たない場合が多く、実際には年々あるいは長期的に変動しうる。例えば、偏西風やモンスーン、ブロッキング高気圧などの自然の気象現象や、地球温暖化・都市化に伴う気温上昇など。

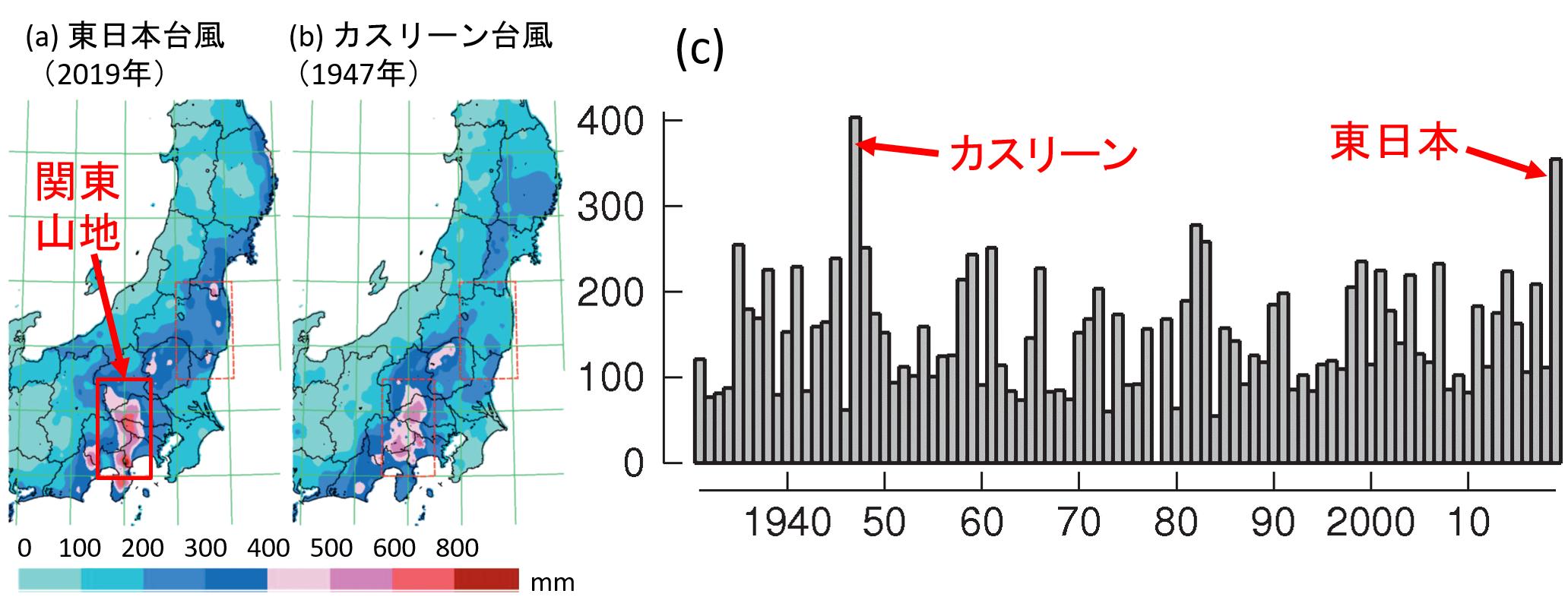
　いずれの不確実性も重要であるが、特に注意が必要なのは(1)である。2020年に起こった台風19号（東日本台風）の気候学的な解析を例に説明しよう^注9）。この台風は、関東甲信越から東北地方に記録的な大雨をもたらして各地で災害を引き起こしたが、これは近来稀に見る台風だったのだろうか？実際に、Gumbel分布による再現期間を求めてみると関東山地では平均で80年に1回起こりうる事象であったことがわかる（表1）。ところが、解析対象期間にはこの台風と同規模の降水量と似た降水分布を示す1947年のカスリーン台風が通過している（図3a, b）。カスリーン台風は、群馬・栃木県で土石流や河川の氾濫や東北地方では北上川水系の氾濫をもたらしたが、試しにこの台風が発生した年を解析対象から外すと、東日本台風の再現期間は107年に増加する。このように、解析の対象期間に「たまたま」カスリーン台風級の大雨が起きたかどうかによって、再現期間の大きさは3割も変わってしまう。

表1　東日本台風による関東山地（図3a）の領域平均降水量の再現期間と推計条件を変えたときの感度。藤部（2020）^注9）から一部抜粋。

図3(a)東日本台風と(b)カスリーン台風通過時の4日間積算降水量の地理的分布と(c)関東山地における過去120年間の日最大平均降水量の経年変化^注9）。

　再現期間は、降水イベントの区切りをどのように設定するかによっても変化する。2日間降水量のデータを使うところを1日間降水量に変えると、東日本台風の大雨の再現期間は578年と大幅に長くなる（表1）。解析期間中の全ての２日間以上にわたる大雨イベントの総雨量が日単位だと２分割されてしまうのに対して、1日の間に完結した東日本台風による大雨の総雨量は減らず、その極端度が際立った結果である。
　降水そのものの地理的なばらつきも、再現期間の推定における不確実要因である。藤部（2020）^注9）の解析では、東日本台風の大雨の再現期間は数100年以上と見積もられる場所もあるが、逆に数10年以下の地点も見られた。このことは、広範囲に大雨をもたらす台風であっても、大雨そのものには地理的に大きくばらつく（局地性が高い）ことを意味する。これを関東山地という「面」で見ると80年となり（表1の基準）、短くはないが空前絶後というほどではなくなる。
　その他にも、測器の変更や観測所の移転、観測時間・時刻の変更などのデータそのものの信頼性に関する問題もある^注8）。
　このように、(1)の不確実性は多様かつ非常に大きいため、極値統計によって推定された再現期間の値そのものを鵜呑みにすることは危険である。
　 (1)以外の不確実性の要因についても触れておく。東日本台風の例では、(2)の不確実性としてGEVを極値分布に用いた場合の再現期間は73年とGumbel分布を用いた場合（80年）が比較されているが、両者の違いは数年であった（表1）。このことは、少なくとも東日本台風のケースでは(2)よりも(1)の不確実性の方が大きいということを示している。また、(3)の不確実性の影響として「異常値」の出現が指摘されている。極値統計理論では、図1cに示した直線によって「普通の」極端気象が現れる確率を予測することはできるが、彦根豪雨のようにそこから大きくかけ離れたさらに極端な極値（異常値）を予測することはできない。図2のリスクマップによると、彦根の日降水量の200年再現値は209 mmであり、彦根豪雨時の観測値（596.9 mm）はその2.9倍に達する。そして、図1cでこの観測値を上へ延ばして赤直線と交わったときの再現期間は「10億年」という非現実的な値になってしまう。このような異常値は、気候の年々変動に伴う大雨の起きやすい年と起きにくい年の差によって出現する可能性があり、現在の極値統計学では扱うことができない^注8）。防災の観点では、異常値こそが大きな災害をもたらしうる重大な事象であり、これを予測することは重要である。しかし、大雨の要因は多様でありそれらと気候変動とを区別することは難しく、今後の研究課題となっている。

４.地球温暖化とは関係なく災害には備えよう

　前節で述べた極値統計学の不確実性を踏まえると、少なくとも再現期間のみからその原因を特定することはできないのは明らかである。近年は、「地球温暖化のせいだ」といえば何でも納得されそうな雰囲気があるが、極端な事象は彦根豪雨のように明治時代にもあった^注8）。気象庁も、数10年程度の期間のアメダスによるデータから、100年に1度の台風なのかどうかなどの長期変化傾向を議論することは原理的に不可能であり、直ちに地球温暖化によるものだとは結論できないとしている^注10）。3章で述べたように、極値統計で推定された再現期間の信頼性は観測期間が再現期間よりも十分に長いときにのみ担保されることを認識すべきである。
　気象庁は、2012年に再現期間50年の48時間降水量などを指標とした「記録的な大雨に関する気象情報」を発表することとしている^注11）。「50年」の基準は、その地域の住民一人一人にとって一生に1・2回の頻度に適合するということであるが、本稿で見たように雨は局地性が強い。このため、たとえ再現期間が数100年以上の事象であっても、数十年に1回はどこかの地点で大雨が起こりうる。50年や100年などの数字そのものに踊らされることなく、忘れた頃にやってくる災害にきちんと備えることが大切である。

【謝　辞】
彦根地方気象台の年最大日降水量データは、気象庁ホームページから取得した。

注1）

岩永哲（2018）広島にとって”未曾有の豪雨”だったのか
https://blogs.rcc.jp/tenki/iwanaga/entry-6614.html#prettyPhoto

注2）

今井明子（2020）温暖化の影響！？「観測史上初」多発の意外すぎる理由
https://friday.kodansha.co.jp/article/136879

注3）

日本河川協会編（1997）建設省河川砂防技術基準(案)同解説（調査編）,技報堂出版, pp. 591.

注4）

Gumbel, E.J. (1958) Statistics of Extremes, Columbia Univ. Press, New York, pp. 396.

注5）

水谷武司（2012）自然災害の予測と対策―地形・地盤条件を基軸として―, 朝倉書店, pp. 306.

注6）

中小河川計画検討会（1999）中小河川計画の手引き（案）～洪水防御計画を中心として～
https://www.jice.or.jp/cms/kokudo/pdf/tech/material/pla-boo-1-01.pdf

注7）

小林健二（2006）確率雨量と再現期間の推定, 測候時報, 73, 51-72.

注8）

藤部文昭・酢谷真巳（2020）極値統計の利用に関する問題, 気象研究ノート, 242, 43-69.

注9）

藤部文昭, 松本淳, 釜堀弘隆（2020）令和元年東日本台風（台風1919）による大雨の気候学的評価―区内観測資料の利用―, 天気, 67, 595-607.

注10）

気象庁（2021）気温・降水量の長期変化傾向　よくある質問
https://www.data.jma.go.jp/cpdinfo/temp/qa_temp.html

注11）

齋藤公一滝, 太田琢磨, 髙橋賢一（2013）50年確率値を活用した記録的な大雨への警戒呼びかけ, 天気, 60, 405-411.