将来の気温変動予測（その１）

－地球気温は上がるのか下がるのか－

2020/09/18

伊藤公紀
横浜国立大学環境情報研究院・名誉教授

序にかえて－将来気温の予測におけるIPCCシナリオについて

　将来の気温や気候の予測は重要だ。しかし簡単なことではない。過去気温の変動についての様々なデータの問題点や、気候モデルの限界などを考慮する必要がある。本稿では、IPCCの報告書(第四報告書AR4、第五報告書AR5)を出発点としつつ、自然変動を考慮して、現在のIPCCとは大きく異なる将来像を提案する。

図1.「将来予測」の例(文献1)

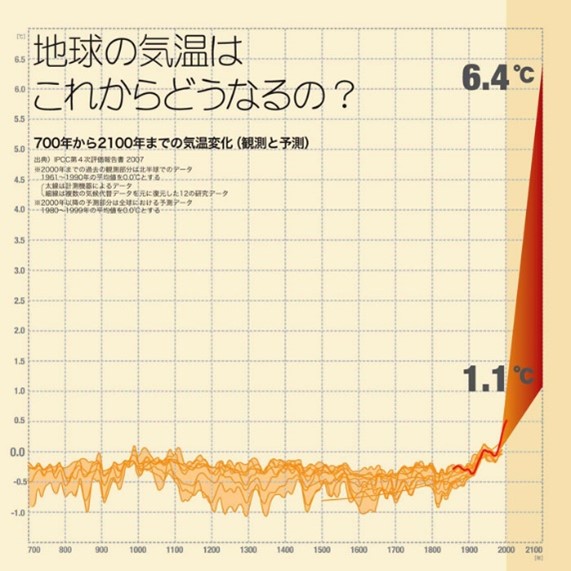
　まず、IPCCが提供する情報を基にした気温の将来予測の例を示す。図1は、IPCC AR4の結果(図2)を総合したもので、「2000年現在の気温は過去1000年の気温よりも高く、2100年には現在に比べて1.1～6.4℃上昇する」との主張だ。まず、この図を叩き台にさせて頂く。

図2.　図1の基になるデータ。IPCC AR4より。左、過去気温再構成データ(WG I Fig. 6.10、文献2)。
右、CO₂排出シナリオと気温変化(Fig. SPM-5、文献3)[拡大画像表示]

　図2左は、過去約1,000年についての色々な気温推定データを重ねたものである。11世紀頃の中世温暖期の気温が現在よりもかなり低いが、このAR4のデータは、IPCC 第三報告書の目玉だった「ホッケースティック曲線」を克服する途中の過程と見るべきであり、そのまま採用はできない(文献4)。
　図2右は、色々なCO₂排出シナリオによる気温上昇である。シナリオB1、A1T、B2、A1B、A2、A1FI における2100年のCO₂濃度は、それぞれ600 ppm、700 ppm、800 ppm、850 ppm、1,250 ppm、1,550 ppmとなる。各シナリオの上にある灰色の棒は、種々のモデルで予想される気温の幅を示している。棒の中ほどにある色付き線は最確値である。図1は、シナリオB1の幅の最低値からシナリオA1FIの最大値までを含んでいることになる。

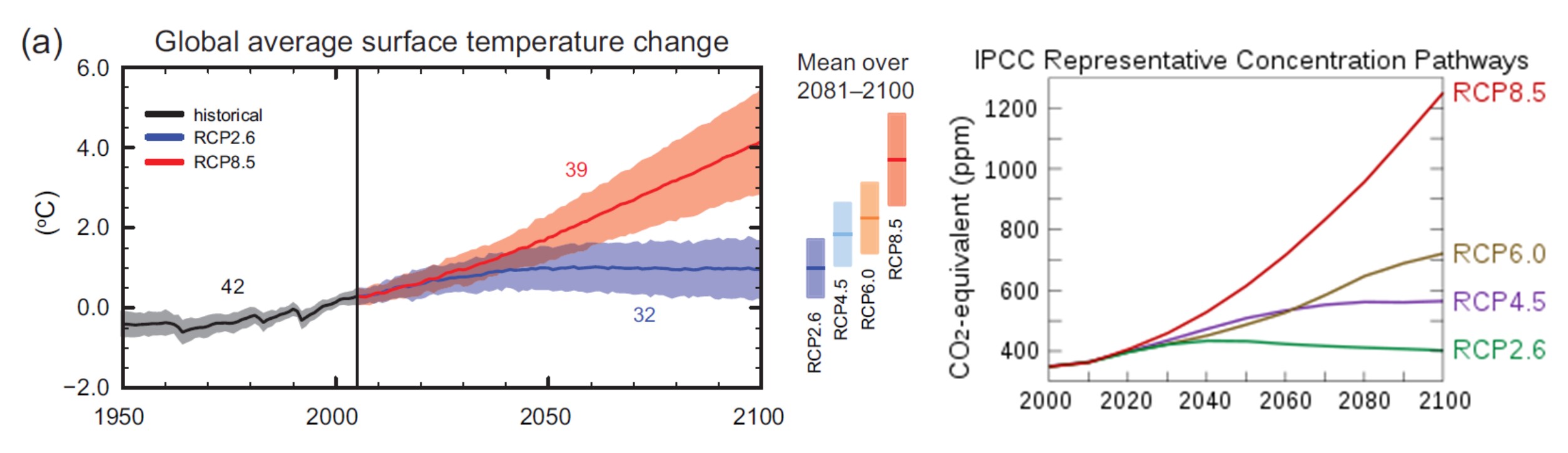図3. IPCC AR5のCO₂排出シナリオと気温上昇(左、Figure SPM.7、文献5)、等価CO₂濃度(右、Fig. TS.19より、文献6)。RCPは、Representative Concentration Pathways (代表的濃度変化経路)[拡大画像表示]

　IPCC AR5では、図3左のような気温変化が予想されている。CO₂排出が大きいシナリオ(RCP8.5)では、2100年には4℃上昇となっている。予想幅が減って、値は多少控えめになったが、AR4のときと本質的なメッセージは変わらない。
　図3右の「等価CO₂濃度」は、メタンなどの温室効果ガスや、エアゾルの冷却因子などを合計して、CO₂の濃度に換算したものである。実際上は、CO₂濃度とあまり変わらないので、以下ではCO₂濃度としておく。
　各シナリオの数字は、2100年時点でのCO₂による「放射強制力」を表す。放射強制力とは、CO₂などの気候因子による加熱や冷却の効果を表すために、対流圏界面(成層圏と対流圏の境目)に熱源・冷却源が二次元的に分布しているように考えよう、というものである。CO₂濃度が2倍になると放射強制力は3.7 W/m²になると見積もられている。RCP8.5では、2,100年に放射強制力が8.5 W/m²　(CO₂濃度は1,250 ppm)となるようにCO₂が排出される。

気候モデルの気候感度について

　放射強制力1 W/m²当たり気温がどのくらい上がるか、というのが広義の気候感度であり、式1が成り立つ。

[気温上昇] = [広義の気候感度]×[放射強制力]　　　　　　　　　(1)

　CO₂による放射強制力は大気中濃度の対数に比例すると考えられている。また、CO₂濃度が二倍になったときの気温上昇を問題にすることが多いので、狭義の気候感度として式2が良く用いられる。

[気温上昇] = [狭義の気候感度]×log₂ ([最終濃度]/[初濃度]) 　　　　　　　　　(2)

　最終濃度が初濃度の二倍になると、気温上昇は狭義の気候感度と等しくなる。以下では、「気候感度」として狭義の気候感度を考える。
　色々な気候モデルが発表されており、それぞれ異なる気候感度を持っているが、IPCCは3℃という値を推奨してきた。これは、CO₂濃度が2倍になった状態が長期間続いて平衡状態になると気温上昇が3℃になる、ということである。
　気候感度の「平衡」と「過渡」の違いは重要である。3℃のような高い気候感度を持つ気候モデルでは、CO₂濃度が二倍になった後も少しずつ気温が上がり、平衡になるのに数十年かかる。そのため、CO₂が二倍になった時点の気温上昇は、平衡での気温上昇よりもかなり小さくなる。この関係を図4に示す。

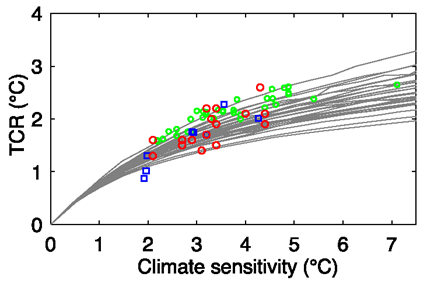
図4.　種々の気候モデルの平衡気候感度(横軸)と過渡気候感度(TCR=Transient Climate Response過渡応答、縦軸)。　(IPCC AR4 WGI Fig. 10.25、文献7)

　図4を見ると、横軸の平衡気候感度が3℃のとき、縦軸の過渡気候感度は1.5～2℃である。6℃や7℃という極めて高い平衡気候感度の場合でも、過渡気候感度はそれほど高くならず2.5℃程度である。この場合、平衡に達するために必要な応答時間は数百年以上にもなる。逆に、平衡気候感度が1℃以下なら応答時間は数年以下で、過渡感度と平衡感度は近い。
　図4の横軸の平衡気候感度は、2℃くらいから7℃くらいまで大きな幅があり、過渡気温感度の幅も大きい。このような気候モデル間の違いは、各モデルが採用する仮定による。例えば米国のミールらは、平衡気候感度が2℃程度のモデル4つを比較した結果、大気から海洋への熱移動の大小が過渡気候感度に1.5℃～1℃の幅を与えているとした(文献8)。
　モデル全般の問題点としては、特に雲と海洋がネックである。海洋は、応答速度に効き、雲は気候システムのフィードバックに効く。
　海洋における熱移動には大小の渦が重要だが、気候モデルに直接取り入れるのは難しい。また雲の中で起きる現象も、微小物理と言われるようなミクロンサイズの過程が重要である。そこまで小さくなくとも、積乱雲など1km以下のスケールの現象は、気候モデルが使用する格子の大きさが例えば数十kmなので直接扱えない。積乱雲は熱帯での気温調整機能を担っていると考えられ、これを間接的にしか扱えないというのは本質的な限界だろう。

次回：「将来の気温変動予測（その２）」につづく。