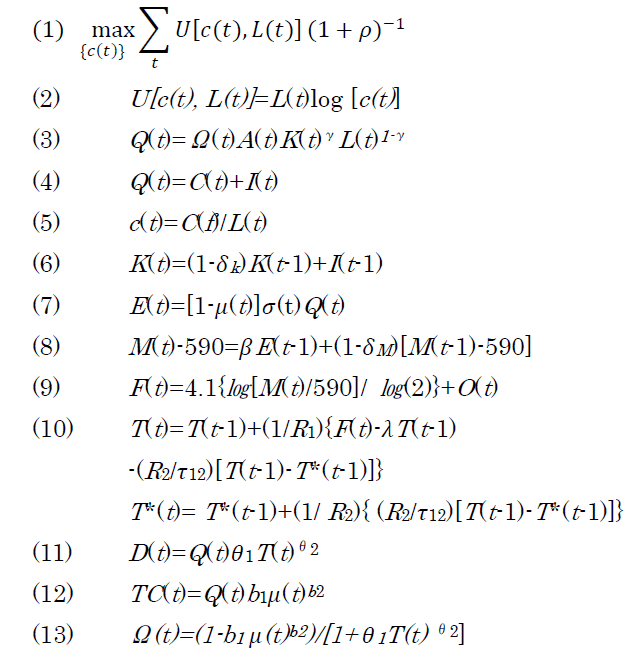ノーベル賞を獲得したノードハウスのDICEモデル

１　はじめに

　2018年のノーベル経済学賞は、ウィリアム・ノードハウス氏に贈られた。氏の最も重要な業績は、「地球温暖化の統合評価モデル(Integrated Assessment Model、IAM)」であるDICEモデル（Dynamic Integrated Climate-Economy、気候と経済の動学的統合モデル）を初めて作ったことである。IAMはやがて今日に至る一大分野となって、地球温暖化問題の理解をおおいに促進した。（なお同モデルの簡単な解説や入手・利用方法については、東大の杉山昌広准教授が解説しているので併せて参照されたい。^注1）
　筆者もノードハウス氏には恩がある。地球温暖化問題を理解するにあたっては、このモデルがおおいに役に立った。それは、物理学の基礎方程式のようにあらゆる検証に耐えるといった性質のものではない。むしろ、一定の考え方の枠組みを示すに過ぎない。だが、対象が地球温暖化という極めて複雑な問題であるからこそ、簡潔な数式でいったんまとめておくことは、後々思考を重ねてゆくにあたって大変に有益なステップとなる。
　そこで本稿であるが、ノードハウス氏が作成したDICEモデルの解説をする。これは13本の式からなる。
　今日では多くのIAMモデルが作成され、それがIPCCのシナリオの作成に使われて、パリ協定での２度目標の合意にも大きな影響を与えた。近年になると、計算機の能力が上がったおかげで、モデルは大いに巨大化・複雑化している。しかしその基本構造は、ノードハウス氏のDICEモデルから殆ど変わっていない。従って、DICEモデルを理解すれば、IAMではどのような議論をしているのか、IPCCのシナリオとはどのような計算に基づいて作成されているのか、よく分かるようになる。
　本稿の最後では、DICEモデルの試算結果の含意について述べる。DICEモデルが出来てから30年近くになるが、今日的な意義を全く失っていないのは驚きである。

２　ノードハウスのDICEモデル

　まずは以下、順を追って13本の式（図表１）を解説しよう。変数の説明、パラメータおよび初期値の設定については図表２、図表３を参照されたい。なお以下は概略を分かり易く説明することを目的にしているので、厳密さは犠牲にしている。正確にはノードハウス氏の著書およびその邦訳を参照されたい(Nordhaus, 1994)(ウィリアム・ノードハウス, 2002)。なおDICEモデルには幾つかのバージョンがあるが、以下では(Nordhaus, 1994)にあるもっとも初期の簡潔なバージョンを紹介する。これ以降にノードハウス氏自身もあれこれ改良を試みているが、本質はこのバージョンで尽きているし、モデルの作りも簡潔で分かりよい。

A 目的関数

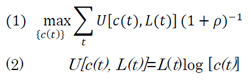
　このモデルでは、世界全体での「効用」を最大化するような一人当たり消費c(t)の経路を探索する。時間tは10年刻みで計算する。効用は、(1)で示されており、世界全体の一人当たりの消費（概ね世界全体の一人当たりのGDPに比例する）の対数に人口を掛けて割引率ρで割り引いたものである^注2）。割引率ρは表２から年率3%と置いていることが分かる。なぜ対数を取るのか、なぜ3%で割り引くか、といった詳しい議論は4章で行う。経済学に詳しくない読者はとりあえず「そんなものか」と思っておいて、先に進んで頂きたい。
　以下に説明するように、最適化するのは、世界全体の投資行動と温暖化対策である。投資行動というのは、投資するか消費するか、という選択のことである。現時点で消費を減らして、多くを投資すれば、その分経済が成長して後々の消費が増えるので、投資と消費のタイミングについてのバランスを解くことになる(下記の「B．経済」が該当する)。もう一つのバランスは温暖化対策に関するもので、現時点で排出削減をすると、コストはかかるが、後々の環境影響による損害を抑えることが出来る。このバランスを解くためには、CO₂が排出された後、大気中に蓄積されて温暖化を起こし、それが存在を引き起こすという一連の式が必要になる（下記「C．気候」と「D．温暖化影響と環境影響」が該当する）。

B 経済

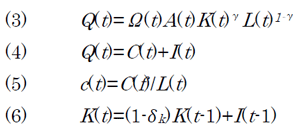
　この４本の式は、(3)式のΩ(t)を１とおけば、経済成長のごく標準的なモデルである。(3)は、経済産出（GDP）が、資本Kと労働Lの投入によって決定されることを示す。この際、技術進歩を示すパラメータAが外生で与えられている。(4)はGDPが消費Cと投資Iに分配されることを示す。(5)は一人あたり消費の定義である。式(6)は資本の蓄積を示す式で、一期前の資本がδ_kだけ減耗するが、当該期の投資Ⅰの分だけ増加する、ということを示している。再び、経済学に詳しくない読者はとりあえず「そんなものか」と思っておいて、先に進んで頂きたい。
　(3)式のΩ(t)の意味は後述の「D.」で述べる。

C 気候

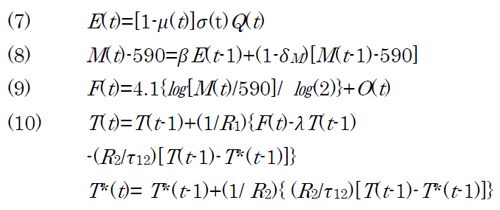
　この一連の式は、温室効果ガスの排出によって地球の温度が高くなるメカニズムを記述している。
式(7)はμ(t)=0と置くと

となる。これはGDP　Qの成長に伴ってCO₂の排出Eが増えることを示している。係数σが掛かっているのは、経済成長に伴って経済がサービス化し、GDPあたりのCO₂排出は減少することを表現している。σは一定の年率で減少するとされている（表２）。μ(t)の意味は「D.」で後述する。
　式(8)　は、大気中のCO₂濃度（濃度といったが、大気中のCO₂の量メガトンMtで表示されている）の蓄積に関する式である。右辺の第１項の βE(t-1)は、CO₂排出量のうち、β（＝0.64）だけが大気中に留まることを示す。残りは地上の植物に吸収される。式(8)からまず見て取れることは、CO₂は年々の排出ではなく、大気中への長年の蓄積があって初めて温室効果をもたらす、いう特徴があることである。
　第２項の(1-δ_M)[M(t-1)-590]は、大気中のCO₂の蓄積量(Mt)が産業革命前の水準である590を上回っているときには、δ_M　ずつ海洋に吸収されて減少してゆくことを示している。表２を見るとδ_Mは0.0833 per decadeとあるから、年率で言うと0.00833であり、逆数を取ると120年となる。つまり大気中のCO₂が海洋に吸収されていく時間スケールは120年程度となり、CO₂は大気中に蓄積される際だけではなく、減少する際にも結構長い時間がかかることが解る。
　式(9)は、温室効果を表す式である。CO₂の蓄積量が増えると、それに応じて放射強制力F(t)が増える。放射強制力とは、ワット／平方メートルの次元を持ち、地球の表面１平方メートルあたり何ワットの温室効果が起きるかを示す量である。これが大気中のCO₂の蓄積量M(t)の対数と、後はCO₂以外の、メタンや代替フロンなどの温室効果であるO(t)の和となっている。
　式(10)は、温室効果がF(t)で与えられたときに、地球の大気と海の温度がどのように上昇するかを示す式である。このモデルでは大気と海を、「上層＝大気および浅い海」および「下層＝深い海」の２層に分けて表現している。そして「大気および浅い海」の温度はT(t)、熱容量はR₁で表されている。「深い海」の温度はT^*(t)、熱容量はR₂で表現されている。
　(10)を理解しやすくするためには、

と置くとよい。これは、２層の間の温度差に応じて、時定数τ₁₂を以て、上層（大気及び浅い海）から下層（深い海）に移動する熱量である。すると(10)は以下のように書き直せる：

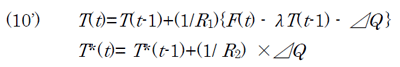
　こうすると、上層の温度T(t)は、温室効果F(t)によって上昇すること、深い海への熱移動⊿Qによって減少することが分かる。下層の温度T^*(t)は、上層からの熱移動の分だけ増大する。
　右辺でまだ説明していない項にあるλは、フィードバック・パラメーターと呼ばれる。温度Tが上昇すると、２つのことが起こる。第１に、宇宙への放熱であるプランク輻射が増える。これによるλへの寄与は正の符号になる。第２に、温度Tが上昇すると、大気中の水蒸気の量が増える。これはクラウジウス・クラペイロンの式に従って、大気中の飽和水蒸気圧が上がるからである。水蒸気は温室効果ガスなので、これは温度を上昇させる。つまりこれによるλへの寄与は負の符号になる。さらに、水蒸気が増えると、雲が増える。雲は、太陽光を遮って地球を冷やす効果もあるし（＝直感的に言えば、曇りの日は晴れの日よりも寒い）、地表からの輻射熱を遮って地球を暖める効果もある（＝直感的に言えば、冬の朝は曇りの方が晴れの日よりも温かい）。この雲の挙動がどうであるかということが難題であり、これに関する推計の幅は極めて大きい。
　λ　についての意味を更に探るために、平衡状態を想定しよう。つまりT(t)=T(t-1) かつT^*(t)= T^*(t-1)とすると、定義により⊿Q =0　となって、(10’)は

となる。さて、大気中のCO₂濃度が産業革命前の２倍になったときの平衡状態の温度上昇を「気候感度 climate sensitivity」と呼ぶ。これは、CO₂濃度が２倍になったときの放射強制力F_2xを用いて
F_2x – λ ×　climate sensitivity=0、ということなので、変形して、
climate sensitivity　= F_2x / λ
となる。気候感度は本質的にはフィードバック・パラメーターの逆数、ということである。この気候感度について2013年のIPCC第５次報告書では、1.5℃と4.5℃の間に入る確率が66％以上、とされている。随分大きな科学的不確実性がある。これは、フィードバック・パラメータ―λに大きな不確実性があるためであり、その理由は水蒸気と雲の挙動についての科学的理解が不足していることによる。
　さて、地球温暖化問題の特徴として、CO₂が蓄積されて温室効果の強さFが大きくなるにも時間がかかることは既に述べたが、これに加えて、Fが大きくなってから温度が上昇するまでの間にも時間遅れが生じる。この時間遅れが生じるのは、地球の熱容量が大きいからである。この大きさの感覚をつかんでおこう。
　表２を見ると、
R₁=13.2 watt-years/m²/degree C
R₂=223.7 watt-years/m²/degree C
　となっている。これは、上層（空気と浅い海）は、流入する熱量が1watt/m²の場合には、1℃温まるために13.2年かかる、という意味である。下層（深い海）は、浅い海からの熱の流入が1 watt/m²の場合には、1℃温まるのに223.7年かかるという意味である。海は平均の深さが4000メートルもあり、水は空気の４倍の比熱があるので、深い海まで温まるのには随分と時間がかかる訳である。
　以上はパラメーターの話であったが、もう少し量的感覚を掴むエクササイズとして、モデルの中で少しだけ数字を追いかけてみよう。
まず(10’)でF(t) -⊿Q＝０と置くと、

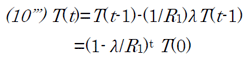
となって、時定数R_1　/　λで温度は下がっていく。表２の値を用いるとこの時定数は31.4年となる。つまり放射強制力と海洋の熱吸収がバランスしている状態（F(t) -⊿Q＝０）では、上層（大気と浅い海）の温度は時定数31.4年で減少してゆく。大気と浅い海の温度はだいたい30年ぐらいで冷える、ということだ。
　次に、深い海を見てみよう。既に出てきた式

で、最近の観測値である⊿Q=0.5watt/m2 程度を入れてみると^注3）、表２からR2=223.7 watt-years/m2/degree Cであるので

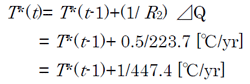
つまり今のペースだと深い海全体が１度温度上昇するには447年かかることになる。深い海はやはり温まるのに相当な時間がかかることが解る。

D 温暖化対策と環境影響のコスト

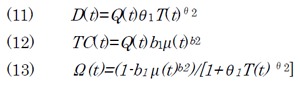
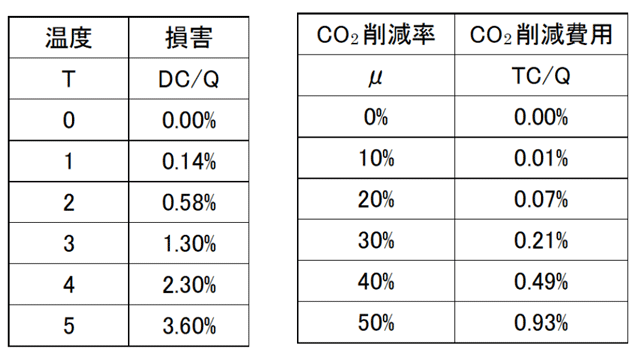
　式(11)は地球温暖化による環境影響がもたらす損害D(t)の式である。これはGDP Q(t)　に比例して発生し、その係数は　θ₁T(t)^θ2となっている。表２を見ると、これは２次関数になっていて、温度上昇が１度のときの損害がGDPの0.144%であり、温度上昇が２度のときの損害はこの４倍の0.576%となる。
　式(12)はCO₂を排出削減する為のコストTC(t)である。これもGDP Q(t)　に比例して発生し、その係数はb₁μ(t)^b2となっている。表２を見ると、これはほぼ３次関数になっている。ここでのμ(t)の意味であるが、式(7)を見ると、CO₂の削減率であることが分かる。つまり例えばμ(t)＝10%であればCO₂の削減率は10%ということになる。
　式(13)の意味であるが、Ω(t) は、GDPへの環境影響による損害（式11）および排出削減によるコスト（式12）から合成された係数である。これが、式(3)のように、GDP Q(t)を減少させる。

図表１　ノードハウスのDICEモデル
出典：　(Nordhaus, 1994) p19より筆者作成

図表２　DICEモデルの主要な変数
出典：　(Nordhaus, 1994) p20

図表３　DICEモデルにおけるパラメーターと初期値
出典：　(Nordhaus, 1994) (p21, p

３　試算結果の例

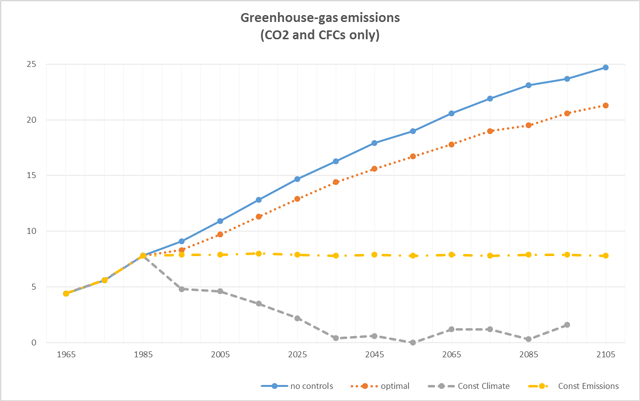
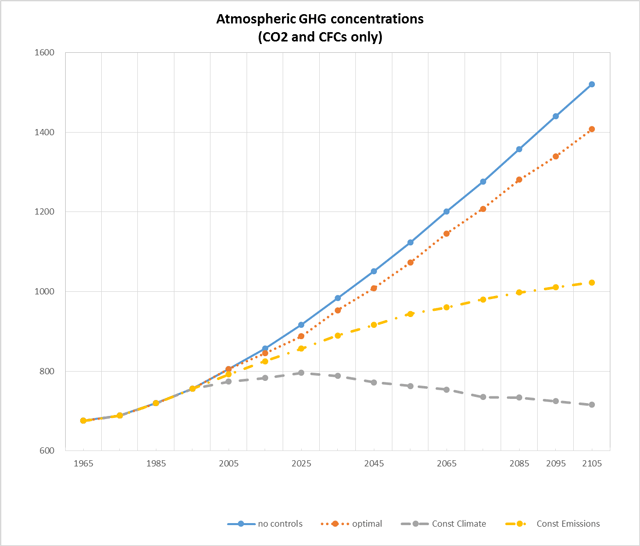
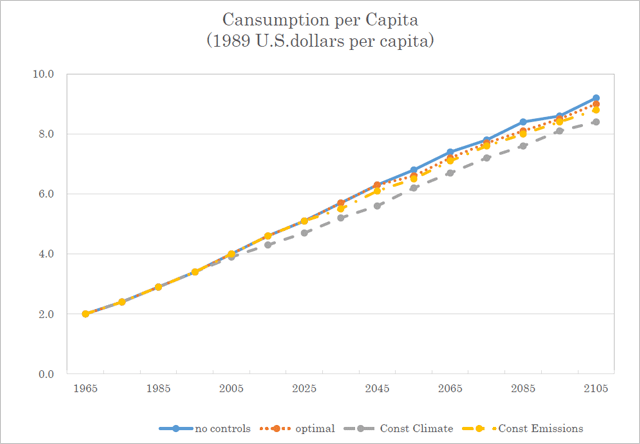
　モデルを走らせた結果が図表４（CO₂排出量）、図表５（大気中のCO₂濃度）、図表６（温度上昇）、図表７（一人当たり消費）である。２章で紹介したモデルの解は”Optimal（最適解）“として示されている。他に３つの線があるのは、比較対象のために設定された別のケースである。
　No Controlは、温暖化対策をしないもの。２章の一連の式にμ(t)=0　という制約式を追加して計算することで解が得られる。
　Constant Emissions とは、図表４のように2000年以降一定値以下に排出量を抑制するもの。これはいったん、２章の一連の式で最適化して、1990年のCO₂排出量E^＊を求めてから、E(t)< E^＊　という制約式を追加して再計算することで解が得られる。
　Constant Climate とは、図表６から分かるように一定水準以下に温度上昇を抑えるケースで、ここでは1900年を基準として温度上昇を1.5℃以下に抑える、としている。２章の一連の式にT(t)<1.5　という制約式を追加して再計算することで解が得られる。

図表４　CO₂排出量
出典：　(Nordhaus, 1994)より筆者作成

図表5　大気中のCO₂蓄積量
出典：　(Nordhaus, 1994)より筆者作成

図表６　温度上昇
出典：　(Nordhaus, 1994)より筆者作成

図表７　一人当たり消費
出典：　(Nordhaus, 1994)より筆者作成

４　議論

　このDICEモデルを一たび理解すると、これを足掛かりとして、様々な議論――実際のところ、温暖化問題に関するあらゆる議論――が出来る。本格的に始めると本１冊でも足りないが、以下では、幾つか重要と思うポイントを指摘しよう。

地球温暖化問題の全体像

　DICEモデルの最大の意義は、地球温暖化問題を簡潔な１３本の式に纏めたことである。これは地球温暖化問題を総合的に分析する枠組みを与えている。図表１を繰り返し眺めることで、読者はいつでも地球温暖化問題の全体像を思い描くことが出来る。
　また３章で紹介した試算結果も、今日なされている他の複雑なモデルの試算結果と驚くほどよく似ている。例えば図表５は、2014年のIPCC第３部会報告書の図SPM.4と殆ど変わらない。筆者が親しくしている某大学教授は2014年のIPCC報告書を見て、「この人たち、まじめにやっているんですかね。私が20年前にやっていた頃と全然図が変わらないし、言っていることも変わらない。講義をするときも、ノードハウスが使っていた図をそのまま未だに使っているし、変える必要すら全然感じない」、と辛辣なことを（笑顔で）語っていた。ここでは後の人を責めるよりは、それだけノードハウスが本質を突いていたことを称賛したい。

不確実性は大きい

　更に議論を進める前に、DICEモデルの弱点について（というより、地球温暖化問題についての人類の理解の貧しさについて、と言った方が良いかもしれない）、２点ほど注記をしておきたい。第１に、不確実性である。
　DICEモデルの定式化やパラメーターには不確実性が極めて大きい。気候については、気候感度はIPCCの見積もりでは1.5℃から4.5℃までの幅があるところ、DICEモデルではおおむね中央値である2.9℃と置いている^注6）。
　この誤差幅はかなり大きいように思えるが、実はよくわかっている方であり、他のパラメーターの方がもっと誤差が大きい。例えばCO₂削減の費用TCの誤差はこれより大きいと思う。CO₂の環境影響の費用DCの誤差はもっと大きいことは間違いないと思う。何れも、関数形すら定かではなく（もっと言えば、関数の存在すら定かではなく）、かなり「えいや」と置いたものである。これは今日の他の統合評価モデル（IAM）でも同じことである。経済成長の定式化についても、経済学者はこのように定式化する習慣があるけれども、パラメーターの誤差は大きいし、これまた関数形すら定かではない。DICEモデルもそうであるが、パラメーターを決定する時には一応は統計データで推定し、その際には検定をして帰無仮説を棄却するのが普通だけれども、帰無仮説とは符号は正しいというだけのことで、それを棄却したといっても誤差幅は極めて大きい。それに相関は測定できるが、因果を示すものでもない。そのようにして設定されたパラメーターに基づくモデルは、将来予測において、大きな不確実性を内包することになる。

予言能力は無い

　第２に、予言能力についての但し書きである。
　以上のように不確実性が大きいので、モデル自体に予言能力があるかといえば、あまり無い、といった方がよい。この意味は、例えば、1965年から2000年まででキャリブレーションをして、2000年以降2018年までに起きたことを予言できたかというと、予言の多くは当たらなかったであろう、ということである。
　物理学者ファインマンの言だと、科学の価値は、何かを定量的に予言できることにある、という。もしそのようなテストが課されるならば、DICEモデルは失格であろう。
　ではこのようなモデルの意義は何か。それは、人間の意思決定と関係がある。人間は、絶えず意思決定をしなければならない。温暖化対策をするのか、しないのか、どこまでするのか、どのようにするのか。何もしないというのも１つの意思決定になる。意思決定をするときには、それは有限な時間でしなくてはならない。このような時には、完璧な科学の成立を待つことは出来ない。そこで、可能な知見を動員して、シミュレーションを行い、それを意思決定のためのインプットの１つとして活用することに意義がある。
　ただし、大事なことは、かかるシミュレーションは、１つの有益な道具ではあるが、あくまでも科学としては不完全なものであり、その試算結果を正確や予測ないし予言であるかのように思ってはならない、ということである。^注7）

驚愕の結論：　最適解は「温度安定化」よりも「何もしない」に近い

　但し書きが終わったところで、試算結果で、最も注目すべきところを述べよう。
　図表４、５、６、７を見ると、CO₂排出・大気中のCO₂蓄積量・温度上昇の何れも、「最適解（optimal）」は何もしない（no control）場合に近く、「温度安定化(control climate)」からは程遠い。
　これは驚愕の結論と言える。
　パリ協定で諸国が合意した２度目標は、ほぼここでの「温度安定化(control climate)」シナリオである。しかし、DICEモデルはそうではなく、成り行きに近い方が「最適だ」としている。
　では、なぜこのような結論になったのか？
　ノードハウスの説明は２点にわたる。
　第１に、温暖化対策の費用は、環境影響の費用と、比較されなければならない、ということである。地球温暖化による環境影響があるというなら、それは冷静に温暖化対策の費用と比較をしましょう、というのがノードハウスの考え方だ。対照的に、パリ協定の場合、なぜ２度を目標にしたのか、その根拠は示されていない。筆者の理解では、地球温暖化の被害が２度を超えると大きくなるという証拠は乏しいから、２度を絶対的な目標として、それを達成することが温暖化対策の在り方だとする意見には、やはり違和感がある。この点について詳しくは拙著を参照されたい(杉山大志, 2018)。
　第２に、温暖化対策への投資は、他の経済活動の為の投資と見比べられなければならないこと、である（経済学的には「温暖化対策投資には機会費用がある」と言う）。温暖化対策に投資をすれば、その分CO₂は減って、温暖化による環境影響は減ることになる。しかしそれだけではなく、温暖化対策に投資をするということは、経済成長のための様々な資本への投資（道路、工場、学校、病院等の建設）が減ることになり、現在の人も未来の人もその分貧しくなる。未来のために良かれと思って温暖化対策をしても、それによって貧しくなってしまうのであれば、持続可能な経済開発とは言えない、ということだ。

割引率の問題

　本稿で紹介したノードハウスの計算では、将来の一人当たり消費はおおむね年率4%で割り引かれることになっている。このことが、結論に大きく影響しており、論争の的になってきた。将来の人々の消費の価値を割り引くというのは、妥当性はあるのか、ないしは、不道徳なのではないか、といった批判である。
　先に進む前に、まず、割引率が年率で約4%になっていることを確認しよう。
　式(1)と式(2)を合わせると、一人当たり消費ｃは、二重に割引かれることになる。まず第１に、(1)を見ると、ρで割り引かれている。さらに、cは対数を取っているので、同じ金額の消費でも、豊かになった将来の方が、現在の消費よりも小さく評価されることになる。つまり同じ１円の消費ｃでも、その発生する時刻によって目的関数への寄与には異なるウェイトが付くことになる。時刻tにおいて発生した消費は、log [c(t)] の微係数(=1/c)に比例した分しか目的関数に寄与しない。従って、経済成長率をgとすると、1/c＝（1+g）^-tとなって、つまり目的関数はgで割り引いて評価されることになる。
　因みに以上の説明は数学的に書くと下記のようになる（なおρ、ｇ≪1として２次以上の項を無視する）：

　いずれの計算結果からも、将来時点の消費δcは割引率ρ+gで割り引かれていることが解る。
　さてρをノードハウスは年率3％と置いている（図表２）。ではgは幾らか。図表７を見ると、一人あたり消費cが1965年から2105年までの間に、約４～５倍になることが示されている。ここでは簡単のため４倍としよう。すると、140年間で4倍だから、70年で２倍であり、これは年率g =１％ということになる^注8）。すると、ρとgの合計で、一人当たり消費cは年率４％で割り引かれることとなる。

将来世代は我々よりも遥かに豊かになる

　ノードハウスは、この４％の割引率を、温暖化対策投資を他の投資と見比べる観点から正当化できるとした（＝温暖化対策投資の機会費用の観点から正当化できるとした）訳である。
　この割引率を巡っては、スターン・レポート等から様々な批判があり、ノードハウス自身も反論しているが、ここでは深くは立ち入らない。詳しい論争については(ウィリアム・ノードハウス, 2015)を参照されたい。
　本稿では、１点だけ、４％という割引率で将来の消費を割引くことは一見不道徳に思えるかもしれないが、実はそうでもない、ということだけ述べておこう^注9）。
　まず、４％の割引率を適用すると、将来に起こる温暖化の損害がかなり割り引かれることは事実である。仮に、現在のCO₂削減率が20％で、70年後の温度上昇が３度だとしよう。（２章Cで見たように、CO₂排出に対する気候システムの応答には様々な時間遅れがあるので、損害はかなり遅れて起きる。ここでは大雑把に70年後の損害と比べる）。ノードハウスのDCの式ではTが３度なら1.30%の損害になる（図表８）。これに対してCO₂削減率が20％ならばCO₂削減費用TCは0.07％である（図表８）。こうすると損害の方が随分大きい。しかし、1.30％の損害に対して、４％の割引率を適用すると70年間で16分の１になってしまうので、すると損害は僅か0.08％になってしまう。これはCO₂削減費用TCとだいたい同じになる。
　このように、年率４％で割り引かれるということは、70年間で、価値が16分の１になってしまうことを意味する。16分の1まで将来の損害を割り引いてしまうというと、何か将来世代のことを考えていない、道徳的に肯定できない酷いことのように思えるかもしれない。しかし実は、そうでもない。
　再び図表７を見ると、どのケースでも、将来世代は140年間で現在の４～５倍豊かになっており、今後70年でも２倍豊かになることが再確認できる。筆者は、DICEモデルには不確実性が多く予言能力が乏しい、とは言ったものの、世界全体の１当たりGDPが年率１％で伸びる、という想定については妥当だと思う。過去も１人あたりGDPは、少なくともこの程度は、着実に上昇してきた。経済成長が続いてきた理由は、主には、技術が進歩したことにあるが、技術は一度進歩すると後戻りすることは無く、これが経済成長の原動力になってきた。これは今後も続くだろう。そして、僅か１％の成長であっても、70年たてば２倍豊かになる。このことが、決定的に重要になる。
　２倍豊かになるならば、温暖化の被害によってGDPの数％が減るとしても、それはものの数ではない。ノードハウスの定式化では温度Tが５度の場合にはDCは3.60％に達する。しかし、70年後には所得は倍増している。従って、損害が生じるにしても、所得が200%に増えるところが200×（1-3.6%）=192.8%に増えるにとどまる、ということに過ぎない。将来の人々の方が今より大金持ちならば、今の貧しい人々がコストを支払わず、将来の人々がコストを払うということは、道徳的には別におかしなことではない。よく「将来世代につけを回すな」と言われるが、これは、将来世代が貧しいならば妥当な話であるが、将来世代のほうがずっと豊かならば、付け回すことに道義的責任を感じる必要はない（もちろん、これはIAMという枠組みで費用便益分析をする限りで、かつ、損害費用がそれほど大きくない、という前提のもとでの結論であるが）。

図表８　DICEモデルにおける損害コストDCおよびCO₂削減コストTC
出典：　図表３，４より筆者計算。

５　おわりに

　統合評価モデルで試算する限りは――つまり、温暖化対策投資の機会費用を考慮し、また、温暖化対策費用と温暖化による損害費用を比較する限りは――現時点ないし近い将来において大規模な排出削減をすることは、正当化することは実は出来ない。正当化されるとすれば、地球温暖化の環境影響による損害をかなり巨額に想定する必要がある。しかし現在の科学的知見では、そのような破局的被害があるとは思えない(杉山大志, 2018)。
　また、ノードハウスの計算における４％という割引率は、道徳的に問題があるという訳では無いことを論じた。
　なお、勿論、以上は統合評価モデルという経済学的な枠組みの下での議論に過ぎない。もしも大規模な排出削減を正当化するならば、審美的な理由、哲学的な理由など、何か別の理由が要る、ということになる。ただしこれが説得力を持つことは相当に難しいと思う^注10)。

<文献>

• Nordhaus, W. D. (1994). Managing Global Commons: The Economics of Climate Change. The MIT Press.
• ウィリアム・ノードハウス. (2002). 地球温暖化の経済学. 東京経済新報社.
• ウィリアム・ノードハウス. (2015). 気候カジノ. 日経BP社.
• 杉山大志. (2018). 地球温暖化問題の探究： リスクを見極め、イノベーションで解決する. 株式会社デジタルパブリッシングサービス.
  www.amazon.co.jp/dp/B07L3YVHDZ

注1）

http://pari.u-tokyo.ac.jp/publications/column185.html

注2）

なお(2)のlog [c(t)]はNordhausでは一般化して[c(t)]^1-α-1}/(1-α)と書いてあるが、結局α→1としているので、これはlog [c(t)]としていることになる。煩雑なので、ここでは単にlog [c(t)]と書いた。

注3）

⊿Q=0.5watt/m2の出典については(杉山大志, 2018)第３章２（２）を参照。

注4）

(Nordhaus, 1994)はここの単位を誤っていたので訂正した。

注5）

(Nordhaus, 1994)はここをwatts/degrees C-m²としてあるが、ハイフンが引き算と紛らわしいので割り算の形で書き直した。watt が分子で、分母が degree C とm²である。

注6）

F_2x =4.1 (Nordhaus p41)であり、表２よりλ＝1.41なので、気候感度は4.1/1.41=2.90となる。

注7）

なおDICEモデルについての最も根源的な批判としては、ゲーム理論でノーベル経済学賞に輝いた故トーマス・シェリングが、「あたかも合理的な1人の人間が一生の計画のように世界経済の成長を計画しているという点で根本的に間違っている」という主旨のことをかなり早い段階から述べており、このシェリングの言は正しいと筆者は思う。現実には、もちろん、無数の不合理な（せいぜい限定合理的な）人や組織がばらばらに意思決定をする結果として世界経済は成長する。DICEモデルの２章A.の定式化は、これによってとりあえず投資と消費の配分を表現できるという便法に過ぎないのであって、効用関数の形が対数(=　log c)であることは誰も証明していないし、あるいは効用関数なるものがそもぞも存在することすら誰も示せておらず、その意味では虚構に過ぎない。（しかし、「割引率の問題」で後述するように、結果的に４％という割引率で割り引くこと、GDPのうち一定の割合が投資に振り向けられること、の２点については２章A.の定式化でそれなりに表現されている。このため、DICEモデルの目的である温暖化問題の費用便益の比較には、この２章A.の目的関数の想定はそれなりに役に立つ。）

注8）

成長率の簡単な概算法：　成長率x％が小さいとき、倍増するには約70/x年かかる。成長率1％なら70年で倍増、成長率2％なら35％で倍増となる。

注9）

批判の中には純粋時間選好ρが存在することに向けられるものもある。しかしこれはあまり問題の本質ではない。重要なのは合計の割引率だからだ。ρが嫌ならばそれを消去しても、合計の割引率を4%のままにするような定式化が出来る。それは、効用関数を書き換えることで実現できる。というのは、図表１での効用関数はlog cになっているが、これも「えいや」と置いたもので、特段の根拠はないからだ。効用関数はべき関数で一般的にc^(1-α)/ (1-α)とすることもできて（これも「えいや」だけれども、その「えいや」の程度は対数関数にするのとたいして変わらない）、このときは合計の割引率r＝ρ+αgとなる。ρ=0%としても、α=4とすれば、g=1%のときにr=4%となる。

注10）

なおノードハウスの最新書(ウィリアム・ノードハウス, 2015)における議論について付記する。
IAMで費用便益分析をする限り「ただちに大規模な排出削減をする」という政策は相変わらず支持されていない。国際協調が限定的にしか起きないという前提（本稿では触れなかったがこれも重要な分析である。国際協調が上手くいかないかもしれない、とい想定は、残念ながら、米中新冷戦などで現実味を増していると筆者は思う）のもとでの「最適解」では何と温度は3.8℃(!)まで上昇する、となっている（p265）。割引率についてはスターンとの論争などを紹介しつつ、相変わらず４％程度が妥当だとしている（第16章）。ただし破局的な被害が生態系に及ぶことは心配していて、それを取り入れると野心的な目標も肯定されうるとしている(p269)。だがその破局的な被害が何なのかは分からない、としている上に、ここでの分析は事実上折角作ったIAMに温度上昇の上限を付け加えているだけなので、IAMの自己否定になってしまっていると筆者は思う（ノードハウスはそうは言っていないが）。
ノードハウスは「臨界点」という表現で、破局的な温暖化影響が出ることを心配しており、それが２℃といった野心的な目標も肯定しうるという意見になっているようだが、この点は筆者の見解は異なる。地球温暖化が人類や生態系にどの程度の環境影響を及ぼすかということに関するシミュレーションをどのぐらい信じるかという点において、かなり信じているノードハウスとあまり信じていない筆者の違いがあるようだ。なぜ筆者があまり環境影響評価のシミュレーションを信じていないか、詳しくは(杉山大志, 2018)を参照されたい。
またノードハウスは一貫した環境税（＝炭素税のこと）論者として知られているが、これは、１）温暖化対策はすべきである、２）自動車の燃費規制や再エネの補助金などの規制・補助金で温暖化対策をしようとするとコストが嵩むから反対、３）したがって環境税（ないし排出量取引）がよい、という文脈である(p330)。従って、日本の現状のようにすでに規制やエネルギー税が多々ある状況であれば、それに上乗せする形で環境税を入れるべし、とは言っていない。むしろ、既存の再エネ補助やエネルギー利用に関する規制、エネルギー税を抜本的に見直して（というより廃止して）、環境税で代替すべし、という主張だと理解すべきである。
なおノードハウスはCCS導入のためにも環境税が有益という意見を出しているが(p358)、CCS導入のためにはCCSを対象とした技術開発・実証の支援策を採用すべきであると筆者は考える。なぜなら、環境税となると経済全体を対象とすることになるから、CCSへの投資を正当化するような高い税率を維持することは政治的に極めて困難である、と考えるからだ。ここも意見が合わない。